googlevur.blogg.se

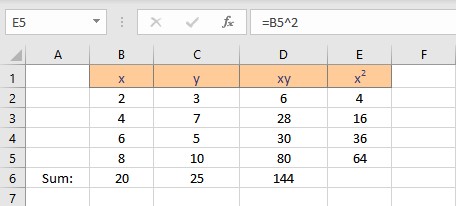
The formula to compute the parameter estimate is In order to use this sample to make educated guesses about the relationship between the two variables (months of machine ownership and time spent exercising) in the population, you need to rewrite the equation above to reflect the fact that you will be estimating population parameters:Īll you have done is replace the intercept ( a) with β 0 and the slope (b) with β 1. Suppose that your ten exercise‐machine owners were randomly selected to represent the population of all exercise‐machine owners. Regression is an inferential procedure, meaning that it can be used to draw conclusions about populations based on samples randomly drawn from those populations. If no single line can be drawn such that all the points fall on it, what is the “best” line? Statisticians use the line that minimizes the sum of squared deviations from each data point to the line, a fact that will become clearer after you compute the line for the example. The regression procedure fits the best possible straight line to an array of data points. Returning to the exercise example, you observed that the scatter plot of points in Figure Where y is the variable on the vertical axis, x is the variable on the horizontal axis, a is the y‐value where the line crosses the vertical axis (often called the intercept), and b is the amount of change in y corresponding to a one‐unit increase in x (often called the slope). When there is only one independent variable and when the relationship can be expressed as a straight line, the procedure is called simple linear regression.Īny straight line in two‐dimensional space can be represented by this equation: It also can be used to predict the value of one variable based on the values of others. Regression is used to assess the contribution of one or more “explanatory” variables (called independent variables) to one “response” (or dependent) variable. To describe the linear association between quantitative variables, a statistical procedure called regression often is used to construct a model.